Physics
Complex problems usually have simple solutions.
Therefore it is not the solution that matters,
but the journey through unknown territory that leads to it.All textual links in this page, except those with the prompt (this link is integral to the text), are best ignored at first.
Physics is, perhaps, as old as the humanity itself, and it too has gone through a number of recognisable evolutionary stages. The first of these, which distinguished physics from other human arts and crafts, may have occurred around 3000 BC in astronomical observations carried out in Egypt, Mesopotamia, India and China. These observations also appear to be the first recognisable scientific activity of the human awareness of nature. From those fragments of ancient history available to us, it is possible to guess what really led to it. Firstly, there were good practical reasons that were helpful to the human survival and prosperity; time keeping for activities such as farming and making astrological predictions appear to have ranked foremost among these. Secondly, faced with the harsh reality of nature, the ancients may have found solace in the thought that astronomical observations enabled them to commune with the heavenly activities and thereby remain just that much closer to the home of the gods that sparkled in the sky night after night.
Heavenly astronomy had an unsuspecting earthly companion which was geometry, the art of measuring the earth. Practical geometry began in ancient Egypt as rope-stretchers annually re-established the boundaries of the farmlands that were flooded by the river Nile and it gradually became a refined tool in the construction of the Egyptian pyramids. However, geometry remained a mere practical tool until the Greek civilisation, which appeared around 800 BC, distilled it into an abstract form. The process of deductive reasoning, which promotes a healthy curiosity of the knowable in place of a morbid fear of the unknowable, is the principal character of the next stage of physics.
Around 600 BC it appears that the human perception of the universe began to change radically, profoundly and decisively. The epicentres of this change were in India, China and Greece. Around this period, these countries produced men who saw the universe not as a chaotic playground of numerous capricious gods, but as an orderly cosmos which functioned harmoniously with all living things. In India and China, the vision was sudden and metaphysical, but in Greece, the new vision of the universe developed much more gradually, involved generations of thinkers, and had the strong undertones of a study aimed at a detailed exploration of the material aspect of the universe. In laying the foundation of this study, all they had was their imagination, and they unleashed it in a torrent of magnificent ideas, some of which continue to hold their ground to this day.
The gradual process of philosophic change in Greece began with the revolutionary thoughts of a Milesian intellectual giant called Thales (c. 624 - 546 BC). Thales primary aim was to replace the supernatural with the natural through observation and experiment, but his lasting contribution was converting geometry from an art of measurement into an abstract science of deduction based on general propositions; those given below are attributed to him.
An isosceles triangle has two similar angles at its base. (The word similar suggests that Thales may not have been able to assign a magnitude to angle).
The opposite angles at the intersection of two straight lines are similar.The base and the two angles at its ends determine a unique triangle.
A circle is divided into two equal parts by a diameter.
A diameter of a circle subtends a right angle at any point on the circumference.
Although such knowledge of geometry is rudimentary and obvious to us now, it must have been an enormous feat of imagination at that time.
The next Greek thinker who made a substantial contribution to physics was Pythagoras (c.570-500 BC), from Ionia. He and his followers made a truly fundamental discovery in geometry which has become known as the 'Theorem of Pythagoras'. It says that 'the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides'. Pythagoreans were said to be the first to have imagined that the earth and all other heavenly bodies had spherical shapes. They also believed that the earth, the sun and the other planets all moved round a 'central fire' and that these movements were accompanied by an inaudible music which they called the 'harmony of the spheres'. They taught that light consisted of particles which travelled from an object to the eye.
At the end of about one and half centuries of existence the Pythagorean school started to dwindle, and around 380 BC a new Athenian school, called the 'Academy' arose. The founder of this school was the Athenian philosopher Plato (429-347 BC) in whose fertile mind mathematics, and in particular geometry, soared to the heights of divine knowledge. To Plato and his followers, abstract geometrical forms became the true substance of the universe, and the 'Academy', which lasted for nearly a thousand years, boasted above its entrance door the motto 'Let none but mathematicians enter here'. Naturally, geometers fashioned the heavens using abstract geometrical forms, and astronomy and geometry finally shook hands.
By the middle of the fourth century BC, science in Greece had begun to decline, and, in about 300 BC, the centre of scientific excellence moved from the Academy, in Athens, to the Temple of the Muses, the equivalent of a modern university, in the city of Alexandria, Egypt. It was here that Euclid (c.330-275 BC) produced his 'Elements of Geometry' which consisted of a coherent treatise of thirteen books on geometrical 'truths' which may be regarded as the real foundation of the physical sciences. It was also here that the great mathematician, Archimedes (287-212 BC), had his education before returning to his native Sicily. Then there were the four great astronomers; Aristarchus of Samos (c.310-230 BC), who proposed a heliocentric solar system; Eratosthenes (c. 276-195 BC), the chief curator of the library of Alexandria, who was the first to measure the distance between the sun and the earth to a reasonable accuracy and was also said to have measured the 'obliquity of the ecliptic' or the tilting of the earth's axis of rotation which causes the seasons; Hipparchus (c. 190-120 BC) of Nicaea who discovered and estimated 'the precession of the equinoxes', or the minute wobbling of the earth's axis of rotation; and finally Claudius Ptolemy who produced an extensive treatise on mathematics and astronomy. This treatise, which became known as Almagest consists of a collection of thirteen books and describes a geocentric universe which, although completely erroneous, remained in authority until the sixteenth century AD. Science continued to flourish in Alexandria until the Dark ages began about 400 AD, when it became virtually dormant for a full thousand years.Around 1400 AD, concurrent with the literary renaissance in Europe, science awoke from its slumber and the third stage of evolution in physics began. Many regard Leonardo da Vinci born near Empoli (1452 -1519), who was talented in virtually every field of human endeavour, as the first renaissance scientist; it appears that he studied nature in the same spirit as we do now. He had been an advocate of the view propounded by the Greek thinkers Democritus of Abdera (c.470-400 BC) and Anaximander of Miletus (c. 611-545 BC) that the universe is governed by mechanical laws. According to Leonardo, we should base science on observation, discuss using mathematics and verify using experiment. He was of the opinion that scientific certainty can only come from mathematical reasoning.
As we discussed above physics may have stirred to life through cosmic curiosity, but it certainly found its feet through cosmic order. The first detailed and systematic study of cosmic order was the geocentric system of the universe produced by Ptolemy. The Polish astronomer Nicolaus Copernicus, (1473-1543) sought to reduce the complexity of this Ptolemaic system, which consisted of about eighty circles of deferents and epicycles, by placing the sun at the centre of the system, rather than the earth. He worked very hard at his heliocentric model but it never occurred to him to question the prevailing belief in the 'naturalness' and 'inevitability' of the circular motion of planets. Because of this, his model too remained complex; but he managed to reduce the number of circles to thirty-four.
With hindsight we now know that all Copernicus had to do was to abandon circles in favour of ellipses; a minor adjustment which would have reduced the number of trajectories to seven and increased the accuracy of the model beyond all expectations. However, no amount of speculation could have bridged the gap which existed between the circle and the ellipse in astronomy at that time. Masses of accurate astronomical data, a matching mathematical acumen and a monumental perseverance were necessary for this purpose. The man who had the means and the inclination to produce such masses of data and satisfy the first of these three requirements was the Danish astronomer Tycho Brahe (1546-1601). He was weak in mathematics and great in astronomical observations. To obtain better accuracy he used better equipment, repeated a measurement many times over, and obtained their average. Thus, he introduced a new standard of accuracy into astronomical measurements, and to this accuracy he charted the positions of stars and planets for a period of over twenty years. But the analysis of this data was beyond his ken and destiny placed it in the hands of Johannes Kepler (1571-1630), the brilliant German mathematician from Weil near Stuttgart. Only Kepler had the qualities which satisfied our remaining two requirements.In a tireless attempt to fit Tycho Brahe’s observations on Mars to an analytic curve, Kepler shattered the groundless belief that heavenly bodies should, of necessity, move in circles merely because these display an elegant symmetry not found in other ‘ lesser’ figures. He found that all the observations fitted perfectly not to a circle but to an ellipse, a curve which was believed to be imperfect. In 1609 he published his findings in a book called Astronomia Nova in the form of the following two laws, which applied to the orbit of Mars.
The planet moves in an ellipse with the sun at one of its foci.
he line joining the sun to the planet sweeps out equal areas in equal times.
In 1618, in a second book called Epitome Astronomiae Copernicae, Kepler next extended these laws to all the remaining planets, the moon, and the four satellites of Jupiter; in other words to all the planets and the satellites of the solar system known at that time. Again in 1619 he published a third book, Harmonices Mundi, in which he announced the following third law which too applied to all the planets.
The square of the time that any planet takes to describe its orbit completely is proportional to the cube of its average distance from the sun.
In replacing the circular orbits with elliptical orbits, Kepler answered the age-old question of ‘how’ the planets moved round the sun. But in so doing, he naturally raised the question ‘why’ the orbits had to be elliptical and not any other geometrical curve. Of course, the circular orbits, owing to their naturalness, escaped this question completely. The best that Kepler could do was to imagine that whilst the sun provided the motive force for the planets to move round in circles, a force akin to magnetism pushed and pulled the circular orbits into elliptical shapes. More than half a century was to elapse before these qualitative conjectures were to become unnecessary in the face of a superlative theory put forward by Isaac Newton (1642-1727).
Whilst Kepler was discovering the architecture of the solar system, an Italian physicist and astronomer, Galileo Galilei (1564-1642), was investigating motion of bodies by conducting rudimentary terrestrial experiments and, where such experimentation was not possible, by resorting to ingenious thought experiments. Prior to Galileo’s investigations it was believed that the natural state of a body was that of rest and that a force was necessary to keep it in motion. Galileo came to the firm conclusion that rest and uniform motion were indistinguishable from each other if an external reference was unavailable. He also concluded that a force just had the effect of changing these states by producing acceleration. Thus, it was Galileo who first concluded correctly, and demonstrated experimentally, the principle of relativity and the principle of inertia which became corner stones of the early classical physics.
However, being unable to shake off the influence of a prevalent belief that certain motions, such as the fall of heavy bodies, result from a natural tendency that is a factor present in addition to inertia and force, Galileo was never able to state the principle of inertia with clarity. Nonetheless, Galileo was able to shatter the belief that gravity causes heavier objects to fall faster than lighter objects and to state quite clearly that all objects fell at the same rate. Until the time of Galileo, the analysis of the motion of a projectile, which formed an important part of the curriculum of mechanics, remained a daunting and an inconclusive task. Using his insight on inertia and the fall of objects under gravity Galileo was able to analyse this motion correctly.Galileo pioneered the telescopic astronomy, using telescopes he made for himself. It is very likely that his were the first mortal eyes that were able to examine closely the surface irregularities of the moon, the stars which forms the Milky Way, the four satellites of Jupiter, the phases of Venus, and the rings of Saturn. However, he wrongly interpreted the rings of Saturn as two small spherical bodies touching Saturn at the opposite ends of a diameter.
Kepler and Galileo provided the key features of an emerging system of mechanics, of universal applicability, within which all primary physical distinctions between the heaven and the earth were to disappear. The formulation of this system of mechanics needed the insight of a genius of extraordinary talent. This genius was the physicist and mathematician Isaac Newton (1642-1727), from Lincolnshire, England. He reduced Kepler’s three laws into a single universal law, set in a background of three completely general laws of motion, two of which embodied Galileo’s principal discoveries. Newton described this universal system of mechanics in a book published in 1687 under the title ‘Philosophiae Naturalis Principia Mathematica’; of this it can be justly said that, with the possible exception of Euclid’s ‘Elements’ and the English naturalist Charles Darwin’s(1809-1882) ‘The Origin of Species’, no greater scientific work has been produced by the human intellect, before or since. Newton's first law of motion was a succinct statement of the principle of inertia that Galileo almost had within his grasp. It was as follows.
Everybody continues in its state of rest or of uniform motion in a straight line, unless it is compelled to change that state by impressed forces.
Now a body may be at rest or be moving uniformly with respect to some location on the earth, but since the earth itself is moving non-uniformly with respect to the sun, the body has a completely different motion with respect to the sun. As this state of affair could continue, it is clear that motion is not an easy concept to define. Newton was fully aware of this difficulty; as a way out, he defined an absolute inertial frame in terms of the following two postulates.
Absolute space, in its own nature, without relation to anything external, remains always similar and immovable.
Absolute, true, and mathematical time, of itself, and from its own nature, flows equably without relation to anything external.
Newton attributed absolute space to the presence of huge, immovable masses which delimited the universe; a kind of immovable framework within which all movable bodies are to be found. Even Newton himself was ill at ease with this framework and with the absolute clock that ticked away regardless within it but, as there were no alternatives, they became established concepts and held their ground for a period of nearly two hundred years. Having made provisions for substantiating motion, Newton next went on to give a quantitative definition of force in the form of a second law of motion, as follows.The rate of change of momentum of a body is proportional to the impressed force and is in the same direction as this force.
This law also introduced a new concept called momentum and Newton defined it as velocity multiplied by an invariant property of the body that he called mass. Thus it was Newton who introduced the fundamental property of mass to physics. Next, Newton introduced the following third law of motion which completed the general description of force.
To every action there is always an equal and opposite reaction.
Unlike the first two laws that were in the making even before Newton appeared on the scene, this third law was of Newton's own making. This law is a statement of a precise balance that transcends time as the forces therein act instantaneously. As we shall discuss below in due course, what Newton really saw was a transcendental principle of balance that operates timelessly in the physical world. Forces just happened to be the only medium of expression that was available to him in his time.
Newton's system of mechanics and the absolute reference frame, which he defined in terms of rigid measures of space and time, are still in use today as they had been for hundreds of years in the past. However, our present knowledge of the nature of space and time leaves us in no doubt that Newtonian mechanics is only valid for speeds that are very much smaller than the speed of light. At speeds that are significant in comparison with the speed of light, relativity theories take over. According to these theories, which were first formulated by Albert Einstein (1879-1955) in a special form in 1905 and then in a generalised form in 1916, motion is a relativistic concept which did not require the support of an absolute space and time: they, after all, are mere hypothetical concepts. However, a small trace of a similar hypothesis remains in relation to the rotary motion of bodies; this remnant is Newton's belief that the cause of the absolute nature of spin motion lies in distant masses of the universe. We shall see later that the real reason for this difference between linear and rotary motions is that their origins lie in fundamentally different structures of spacetime.The single universal law to which Newton reduced the three laws of Kepler, describes with a high degree of accuracy the universal phenomenon of gravitation; this is the only physical phenomenon which affects and is affected by all material bodies. Starting with cosmic systems of planetary size, the force of gravitation is, perhaps, the only key factor which determines the large-scale structure of the universe. Yet, Newton's law for this force is simplicity itself, and it is as follows.
Everybody in the universe attracts every other body with a force proportional to the product of their masses and inversely proportional to the square of their distance of separation.
Newton's physics, which explained all the cosmic and terrestrial phenomena that were significant in his time, reveals four basic parameters which can remain unaffected by varying physical conditions. These invariant elements of Newton's physical world are the mass, energy, momentum, and angular momentum of a particle of matter. The appearance of these four conservable physical parameters and the associated four laws of conservation marks the beginning of a scientific analysis of the intuitive notion of permanence which we habitually associate with the physical world.
In addition to gravity, there were two other basic phenomena, electricity and magnetism, which had, since about 1600, drawn the attention of physicists. With the availability of Newton's framework of mechanics, and aided by his theory on gravity, electricity and magnetism began to develop as two separate sciences called electrostatics and magnetostatics. From 1821 the English experimental physicist Michael Faraday (1791-1867) began to conduct what we now call electromagnetic experiments, and after a period of about ten years discovered the link between electric and magnetic fields. In the fertile imagination of Faraday the concept of physical field turned from fiction to fact. In 1856, the Scottish physicist and mathematician James Clerk Maxwell (1831-1879) successfully arranged all the available knowledge on electromagnetic phenomena, together with a small but vital contribution of his own, into an elegant mathematical theory on electromagnetism, called Maxwell's theory.
Meanwhile Newton's physics had been evolving and by 1834 it had developed into analytical mechanics. Many eminent people contributed to its growth, notably Leonard Euler (1707-1783), Joseph Louis Lagrange (1736-1813),William Rowan Hamilton (1805-1865) and Jacobi (1804-1851). A fundamental feature of analytical mechanics is that position and momentum replace position and velocity (in Newton's physics) as two independent base states. Thus analytical mechanics gives momentum an identity of its own. Absence of any explicit forces is another important feature which distinguishes analytical mechanics from Newton's physics. A third difference is that analytical mechanics is totally independent of coordinate systems. This feature enables a mechanical system to have coordinates of its own. These coordinates, which are the positions and momenta of the components of the mechanical system, define an abstract space called phase space in which the entire mechanical system appears as a single point. Finally, analytical mechanics is ideally suited for the analysis of complex mechanical systems whereas Newton's physics is not.
For a while it looked as if, within the theoretical framework provided by Newton's gravitation, Maxwell's electromagnetism, and analytical mechanics the physical world was about to unfold itself completely in terms of just two independent basic properties of matter: mass and charge. But that was not to be.
In 1887, Albert Michelson and Edward Morley established experimentally that the behaviour of Maxwell's electromagnetic waves was incompatible with Newton's absolute separation of space and time. In 1905, Albert Einstein (1879-1955) who may not have been aware of the Michelson-Morley experiment formulated a new theory of space-time that resolved this incompatibility and showed that Newton's view of separate space and time is flawed. Two others were individually active in this respect and they were the Dutch physicist Hendrick Antoon Lorentz (1853-1928) and the French mathematician Henri Poincaré (1854-1912). In 1908 the Russo-German mathematician Hermann Minkowski (1864-1909) found the correct interpretation of Einstein’s theory and unlocked its full potential. According to Minkowski’s interpretation, space and time are not separate entities as Newton had imagined, but conditional partitioning of one continuum which we now refer to as spacetime. With respect to this new continuum, the concept of position, which used to consist of just three space-coordinates, becomes broadened and includes the time coordinate on an equal footing. This wider concept of position is termed 4-position or, simply, event. Similarly, velocity and momentum, each of which used to consist of three components, acquire a fourth component and become 4-velocity and 4-momentum, respectively. A technically more correct name for the latter is momentum 1-form. The fourth component of 4-velocity prima facie carries no special significance, but that of momentum 1-form represents the energy of matter. Thus, the energy and momentum of a particle of matter, which are conserved as two separate entities in Newton's physics, become a single conserved entity in Einstein's theory which became known as special relativity. Furthermore, the magnitude of this single entity becomes the energy equivalent of the rest mass of the particle of matter. Thus, in special relativity three of the four conserved entities in Newton's physics unify, but the fourth entity of angular momentum remains separate.
The fundamental changes that position, velocity, and momentum undergo in special relativity are concomitant with the speed of light becoming an absolute entity and occupying a special position in physics as required by Maxwell's theory. More precisely, special relativity is an exposition of the spacetime structure that Maxwell's theory demands and they fit like hand and glove. For, in principle, Maxwell's theory is equivalent to special relativity supplemented by just the Coulomb potential of charge.In 1916 Einstein's thoughts on the nature of gravity led him to a generalisation of special relativity, called general relativity. This generalisation clearly showed that the rigid, flat space-time of special relativity is just the limiting form of a small, local region of a flexible, globally curved space-time. Einstein with his general relativity brought to an end physicists' belief in the supremacy of Euclidean geometry and the uniqueness of the Euclidean straight line, just as Kepler with his 'humble' ellipse brought to an end astronomers' belief in the supremacy of the circle and the perfection of the circular shape. A body, which freewheels along a 'straight' line in the curved spacetime of general relativity, would produce the apparent impression that it is under the influence of an invisible force. Thus, just as Newton's force of gravity explained Kepler's elliptical orbits of planets, Einstein's curved space-time explained Newton's concept of force. With this immense achievement, Einstein showed that the entity that we call the physical field consists of a component that we cannot construct accurately using Newton's concept of force.
General relativity established that the structure of this field component, which forms at least the major part of the large-scale structure of spacetime, originates in an entity called a metric tensor which is present as a continuous distribution (or a field) throughout spacetime. A metric tensor, in general, consists of a set of sixteen numbers. However, a certain property of symmetry that the metric tensor possesses effectively reduces this set to ten numbers. Thus, in relativity theory, an event, which carries a label of four arbitrary coordinates, receives ten more numbers which represent what may be called its metric infrastructure. In a curved spacetime the metric tensor varies from event to event no matter what coordinates are used; in special relativity, it remains effectively constant throughout spacetime.A spacetime endowed with a metric tensor field is termed a metric manifold. The term 'metric' signifies that this manifold is able to produce an objective measure for length that we can transport unchanged from one event to another. Also, in a metric manifold a unique line of optimal length, called a geodesic, exists locally between two arbitrary events. A geodesic is the curvilinear equivalent of the familiar straight line in Euclidean geometry. Since in Euclidean space free motion describes straight lines, it follows that in a metric manifold it describes geodesics. The motion along a geodesic is expressible using either the velocity or the momentum, since we can change these from one to the other using the metric tensor without which the geodesic has no real existence. Thus, in general relativity there is no substantial distinction between momentum and velocity.
At present, general relativity is not fundamentally equipped to assimilaie matter into spacetime, at least not in the way Einstein wanted it, according to his book, 'Out of My Later Years'. Only a conjectural equation that Einstein himself proposed determines the metric tensor field, but only in empty spacetime. Consequently, general relativity is still incomplete and Einstein unreservedly maintained to the very end of his life, that its completion entails just uniting gravitation and electromagnetism in a single structure. Einstein believed that this structure would be the Theory of Everything that happens in the physical world. This website presents a theory called 'Balance' that completely vindicates Einstein's belief. It preserves General Relativity as it applies to empty spacetime intact, but only as far as the metric tensor field is concerned. Speeds at which test particles move in this field are always higher than those that general relativity predicts. However, the discrepancy becomes significant only at distance scales of galactic magnitudes and over.This website presents a theory called 'Balance' according to which the physical universe is the embodiment of a 'unique' state of balance between its global and local, or field and particle, aspects. The theoretical representations of these aspects in this theory are in terms of two respective tensor fields and these are the symmetric metric tensor field in general relativity and an antisymmetric tensor field which is a generalised form of the Maxwellean electromagnetic field.
In contemporary physics, strictly speaking, the global and local aspects of the physical universe are separate. Their structures lie in the symmetric metric tensor field and the Maxwellean electromagnetic field, respectively. These structures form two separate rival schools of thought known as General Relativity and Quantum Mechanics. At present Quantum Mechanics is in vogue and its adherents advocate subsumption of General Relativity into its body; the result would be a particle centred physical world which would multiply abnormal complexities such as those involved in quantum entanglement. There are simple, but compelling, mathematical reasoning, e.g. Hausdorff Space, which suggest that continuation and quantisation which are the substrata of field and particle do, indeed, exist as a syzygy, or an archetypal pairing, and that this syzygy is best reached from its continuity side rather than from its quantum side.
There are two crucial differences between quantum mechanics and the two theories of Newton and Einstein. Firstly, quantum mechanics leaves us with a feeling utter confusion, at best emptiness, whereas the two theories possess an intuitive appeal and a sense of uniqueness in that they rise or fall by their core structures within their areas of applicability. Tinkering with the core structures is not an option. Secondly, whilst quantum mechanics has always been a collective endeavour, each of the two theories has been effectively a personal vision. Perhaps this may mean that in any epoch Truth reveals itself only to one for the benefit of many. That said, we should leave alone the chaotic and vibrant world of Quantum Mechanics, and access its vast superlative knowledge base only strategically and at opportune moments.
Prelude
Physics began with astronomical observations and the ancient astronomers used these to build a model of the solar system based on circular symmetry, which they thought symbolised 'divine' perfection. These astronomers had been the pioneers who explored an uncharted terrain using only knowledge and instruments to match and for that reason, they had no access to the depths beneath its surface imagery. So, they unwittingly left the future of what they had begun in the capable hands of their predecessors, da Vinci, Galileo, Kepler, to name a few. Finally, it was Newton with his three laws of motion and the law of gravitation who brought the ancient dream to life as an order that operates throughout the physical world with clockwork precision. However, laws of electromagnetism were outside Newton's framework as electromagnetic observational data were then virtually non-existent compared to the vast catalogue of accurate gravitational data that was available due to millennia of dedicated labour in astronomy. Inclusion of electromagnetism in the curriculum of physics meant that Newton's physics had to give way to Einstein's Relativity, which first appeared in a special form in 1905 and then in a general form about ten years after. General relativity has yet to realise Einstein's vision of a complete theory of physics wherein gravitation and a generalised form of the Maxwellean electromagnetism meet on equal grounds. This website presents a theory called Balance that finally vindicates Einstein fully.
Along with the emergence of General Relativity (GR) on a foundation of symmetry, a rival emergence, which we now call Quantum Mechanics (QM), took place on a foundation of antisymmetry. The incidence of these two emergences borders on Jungian Synchronicity and is a remarkable demonstration of the validity of Bohr's dictum on opposites, stated at the beginning of the 'About' page. With passing time, GR confined itself to the orderly cosmic domain of the physical world where chaos is secondary, and QM, to the chaotic atomic domain where order is secondary. They have remained just as far apart as their two respective domains, to this day. According to Balance, the reason for this persistent chasm is the failure to establish the 'timeless' symmetry-antisymmetry balance that holds the two domains together in a cast-iron grip at core whence forces originate, but in a feather-soft grip at periphery where motions take place.
We have yet to come across a natural state of symmetry existing at the expense of antisymmetry, or vice versa, that is capable of leading to a truly fundamental theoretical abstraction that can be the ultimate foundation of physics. However, with time such naked symmetries, referred to here as just symmetry for short, found their way into the heart of physics, like in the case of GR and QM, and now symmetry has become the foundation of physics, just as it had been in ancient astronomy. Also the practice of building ‘epicycle’ upon ‘epicycle’ to adjust for the limitations of symmetry is continuing still, just as it had been then, but at an even faster and more furious rate. Such action goes against the grain of our intuition and experience and this website shows that replacing symmetry with balance as the foundation of physics all that we have to do to reverse this trend. Because balance also includes symmetry-antisymmetry together on an equal footing, this action does not abandon symmetry, but apportions it a due place in an improved scheme of things to come so that it would become stronger still, but within its own limits set by the concept of Symmetry Group.
Physical world bears clear evidence that symmetry and antisymmetry in their natural form exist inseparably on an equal footing. The long-range force fields of Gravitation and Electromagnetism, which divide the physical world between them into cosmic and atomic regions, are symmetric and antisymmetric tensor fields, respectively. Of the two short-range force fields, Weak force merges with Electromagnetic force at high energies, and according to Balance, so should Strong with Gravity. Motion of a fundamental particle of matter consists of linear and angular components and these are characteristically symmetric and antisymmetric, respectively. In other words, it is symmetry and antisymmetry operating on an equal footing that hold the physical world together. Fundamental entities of the same type in theoretical physics always have infrastructural components of symmetry and antisymmetry. In the analytical mechanics of Euler, Lagrange, Hamilton and Jacobi, which is an elegant alternative representation of Newton's physics, the kinetic and potential energies (T and V) of a physical system that replace Newton's force are two such fundamental entities. The 'difference' ± (T - V) called the Lagrangian is the antisymmetric component of these two energies, and the sum (T + V) called the Hamiltonian is their symmetric component. These two formulations lead to the same dynamics of the physical system. However, while the differential equations of Lagrangian dynamics are of the second order with respect to time, those of Hamiltonian dynamics are of first order; hence the latter is usually preferred.
We discussed above that GR and QM are representations of a physical world torn asunder as regards its symmetry and antisymmetry. Yet the spell of balance between these opposites is so overwhelming that GR and QM each achieve a semblance of its own symmetry-antisymmetry balance within the framework of analytical mechanics, in a startling fashion. For, while the formal structure of GR is Lagrangian-based, that of QM is Hamiltonian-based. Numerous attempts are being made at present to give GR a Hamiltonian-based formal structure in an attempt to acquire gravity quantisation; these clearly work against balance and hence likely to be counterproductive. Also, if quantisation is a great truth, so is continuation, at least according to Bohr, and to express all fundamental physical phenomena in terms of quanta alone would be wrong.
Isotypic Pairing
Symmetry-antisymmetry, as outlined in the 'About' page, is the first of the three pair-formations that make up the foundation of the physical world. They are special cases of a universal phenomenon of Isotypic Pairing that however has not yet drawn the proper attention of physics; a surprising stance given its pivotal role at every major turning point in the history of modern physics and in its rapid rise to stardom. Modern physics began with the works of Kepler and Galileo; Kepler's was sky-bound and it transformed astronomy by establishing that planets move round the sun along elliptic paths with the sun occupying one of the pair of foci of each ellipse. Galileo's was earth-bound and his brilliant account of Salviati's experiment established that unless a pair-formation exists between the inner and the outer worlds of an observer, a rational judgment of the observer's state of motion remains impossible. This pair formation was the basis of the 1905 paper that established special relativity. Pair formation continued to dominate the progress of physics beyond relativity, as even at the heart of quantum mechanics are pairings, called conjugate variables. Today Quantum entanglement, more than any other phenomenon, beckons our attention to pair formation with its near supernatural character symbolic of the state of unbalance that exists in physics.
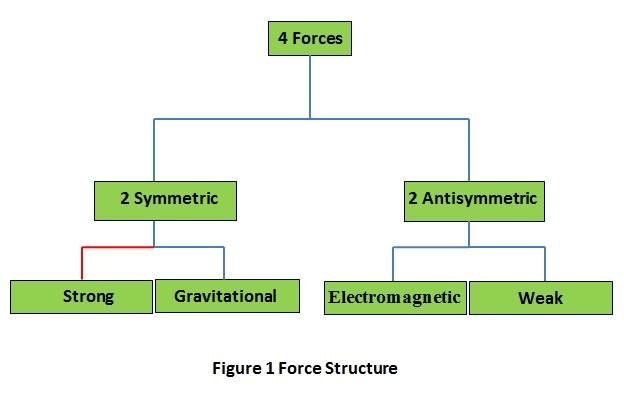
Stable structures, be they physical, biological, mathematical, or otherwise, all have their foundations steeped in isotypic pair-formations. Consider first the field structure of the physical world. In Balance it consists of the pair of fields that are respectively symmetric and antisymmetric in character. Infrastructure of these fields are a pair of symmetric and antisymmetric tensor fields of the same type. The Figure 1 shows how they relate to the existing four forces.
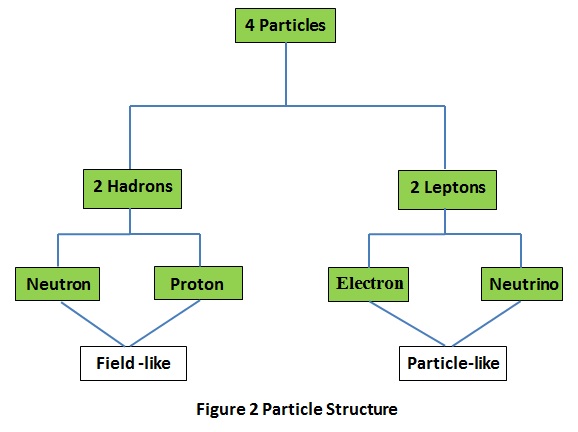
The link between 'Symmetry' and 'Strong', shown in red in the above figure, is yet to establish itself in contemporary physics. In Balance, particles of matter, which are the physical manifestations of the force fields, also pair-form thus.
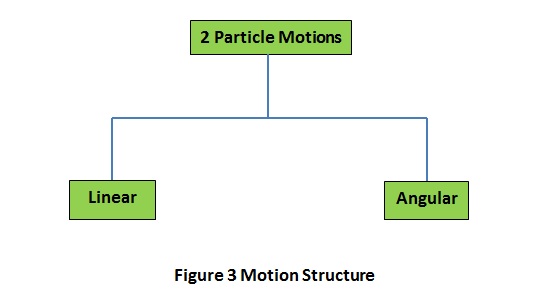
Motion of these particles of matter also pair-form as in the Figure 3.
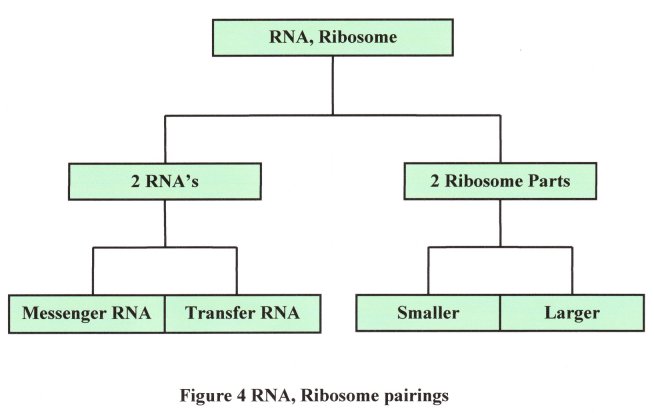
Moving from physical to biological plane, we come across the basic structural units of life, and yet again these DNA (deoxyribonucleic acid), RNA (ribonucleic acid) and Ribosome each exist as pairs of some sort. DNA consists of two helical suger-phosphate back bones joined together by the base pairs, Adenine -Thymine and Cytosine - Guanine. RNA and Ribosome which work as a team to manufacture proteins according to information provided by the DNA, do so by pair-forming as in Figure 4.
Pair formation does not stop with the concrete but extends to the abstract world of mathematics also. The simplest example in this case is the complex number, a pair formation between two real numbers, which to a real number is, so to speak, as human being to ape. An abstract example of a different kind is the pair formation between an event and a set of coordinates.
The physical world has an irrefutable objective character in spite of what quantum mechanics would have us believe, if by objectivity is meant material existence unaffected by the subjectivity of life that probably is related to the 'selfish gene'. In the absence of such objectivity, how could we explain the pre-biological period of the universe in which matter had been present in a very 'stable' form just as not only matter but also as interrelated assemblages in states of dynamic activity ranging from the infinitesimally small to the infinitely large. However, there is evidence that the gene scene is an integral part of the physical world and the present physical form of this evidence is an extreme fine-tuning of the latter just so that the former would eventually appear (strong anthropic principle). However, even millennia after the appearance of life (on earth), there is this macrocosm of staggering proportions in comparison to which that life is still virtually nonexistent and would continue to be so for the foreseeable future. Also here is this microcosm which appears to carryon in blissful ignorance of interference from the subjectivity of life, as evinced by the objective stability of chemical elements and compounds that exists side by side with the subjective element of life. I, of course, can move matter around wilfully but that does not count as a fundamental interaction that disturbs the objective character of matter, as by my action I cannot wilfully change the basic structure of fundamental particles of matter, whatever that may be. My will to change things is a dimension that I possess in addition to those that the physical world possesses. I can only change the field in which particles sit and therefore I conclude that while my physical body is obviously particle-based, my mind is field-based. The archetypal physical field is gravity, and gravitational structure possesses a fundamental feature of arbitrariness that may act as the niche for a feature that is integral with the physical world and yet has a 'mind' of its own.
Those of us who believe that mind is simply a product of the physical world may think that the contents of the preceding paragraph support their belief. That, of course, would be the case for a self-contained physical world. Although the concept of 'self-containment' as in the case of axiomatic systems appears prima facie self-explanatory, Kurt Gödel in his seminal paper titled 'On Formally Undecidable Propositions of Principia Mathematica and Related Systems' showed that reality is quite different, indeed. Gödel proved that any non-contradictory system of mathematics, broad enough to contain at least arithmetic, is not self-contained as it can produce results that are not contained within its framework of axioms and procedural rules. In short, their validity is ‘undecidable’ within the system itself. The most curious of these ‘undecidables’ is the system consistency of the axioms themselves. Therefore, even if the physical world is expressible as an axiomatic mathematical system, for example special relativity, it will still not be self-contained, or even self-consistent. In other words, there is a great deal more to reality than what a physical world by itself can provide, even if one were to exist by some chance.
Now consider the behaviour of light; in relation to the physical world, it is ’immovable’, in that its motion is unaffected by the motion of matter. In addition, it only makes a point contact with the physical world, as the 4-dimensional distance that it travels in the physical world is always zero. Also its composition is quite different from that of matter; bosons vs. fermions. These are the characteristic features of the fulcrum in an old-fashioned balance, indicating that light can act as the fulcrum should there be a state of balance that rules the physical world. There indeed is such a state with light as the fulcrum, and this role of light is established and described in mathematical details in the ‘Theory’ pages. It also becomes clear therein that the entities which are being balanced are field and particle, or simply spacetime and matter.
The role of light as a fulcrum opens up a world of reality that is distinctly different from the physical world and there are indications, albeit intuitive, that it does so together with the stuff that we call mind. This world then functions as the fulcrum for the field-particle physical balance, with light taking up its position as pivot and mind-stuff as base. All these unmistakably point to an almost esoteric objective character of the physical world, and it appears that modern physics has attempted to capture it rationally using the concept of 'symmetry', or more precisely , as the nucleus of rationalisation.
As mentioned at the outset, symmetry has an equal companion which is antisymmetry. For example, symmetry and antisymmetry are respectively the basic characters of the long range force fields of Gravitation and Electromagnetism which divide the physical world between them as cosmic and atomic regions respectively. On an abstract note, a general vector field which is the most basic concept in classical physics is determined by the 'Div' and the 'Curl' where the former represents symmetry and the latter, antisymmetry. In both these examples it may be said that symmetry and antisymmetry are on an equal footing. However Symmetry Group disturbs this equality in the sense that symmetry is made to become a function of a contrived antisymmetry. For, a Symmetry Group operation is always associated with its reverse operation thus making Symmetry Group operations antisymmetric and it is this antisymmetric group of operations which captures symmetry. The proper antisymmetry which complements symmetry is now completely decoupled from it and is relegated to the background. In the case of the long range forces, proper physical antisymmetry which characterises the atomic region of the physical universe now operates remotely from symmetry which characterises the cosmos; hence the past and present failures to join together quantum mechanics and general relativity in spite of sustained and strenuous efforts. So, Symmetry Group has considerable limitations, however, it is also indispensable where it matters as its persistence in physics indicates.